摘要
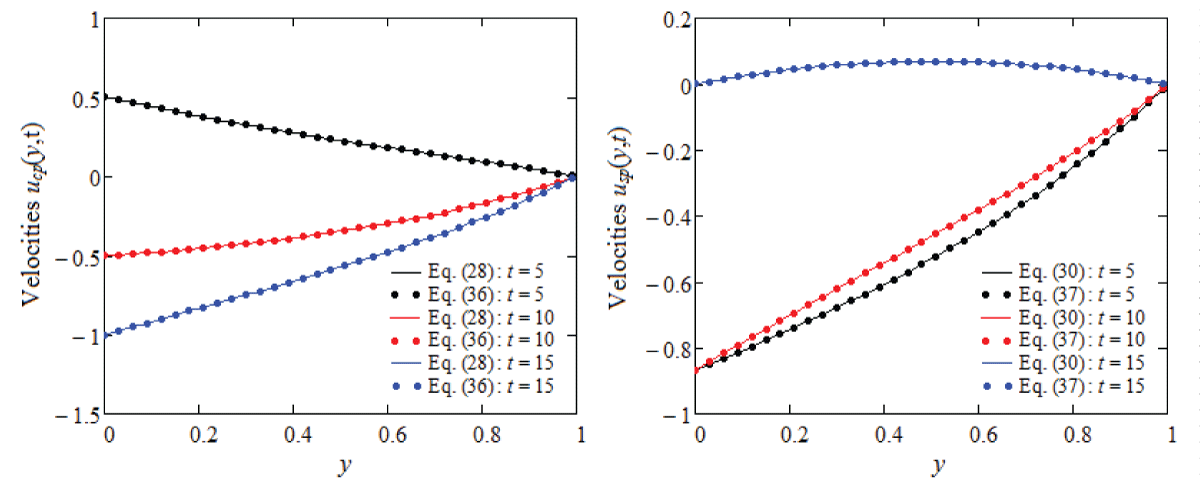
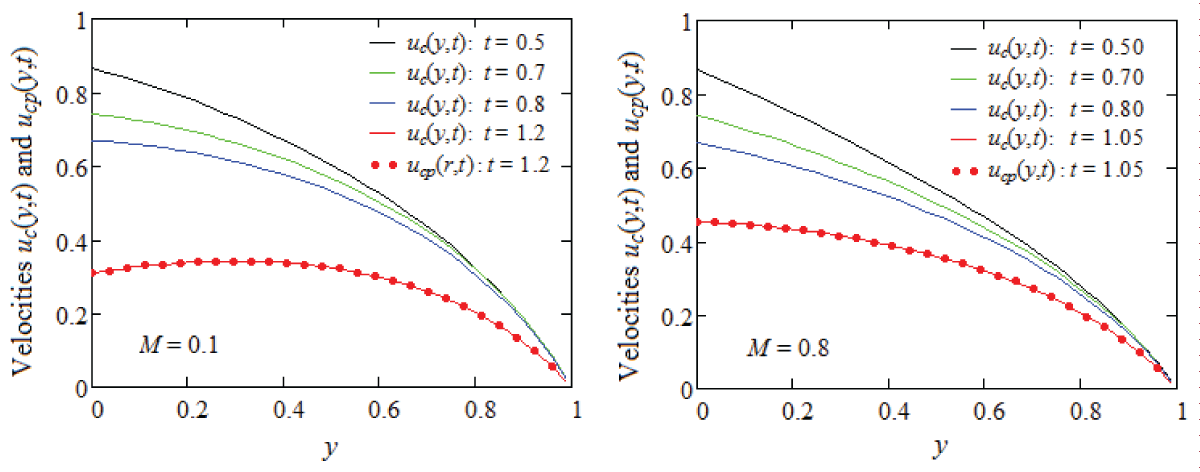
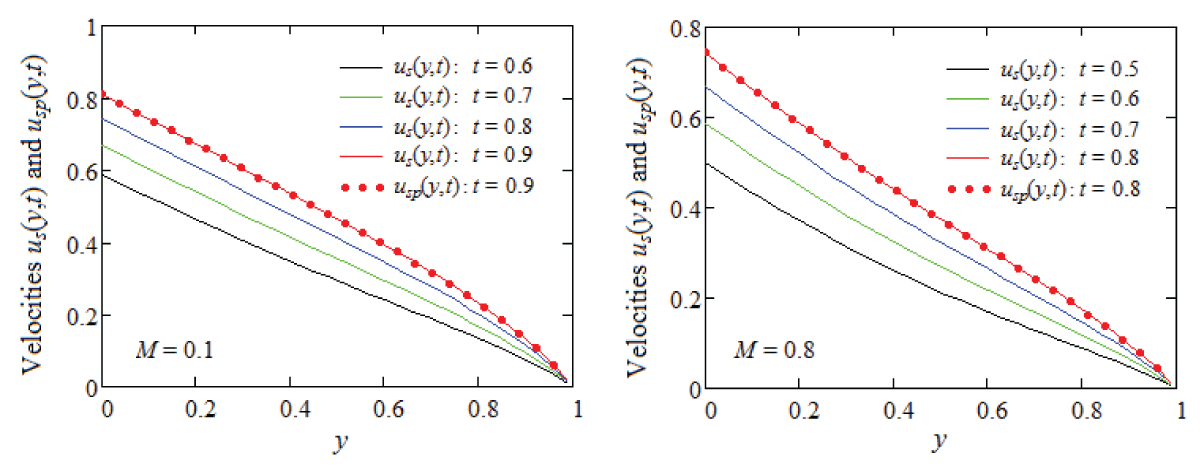
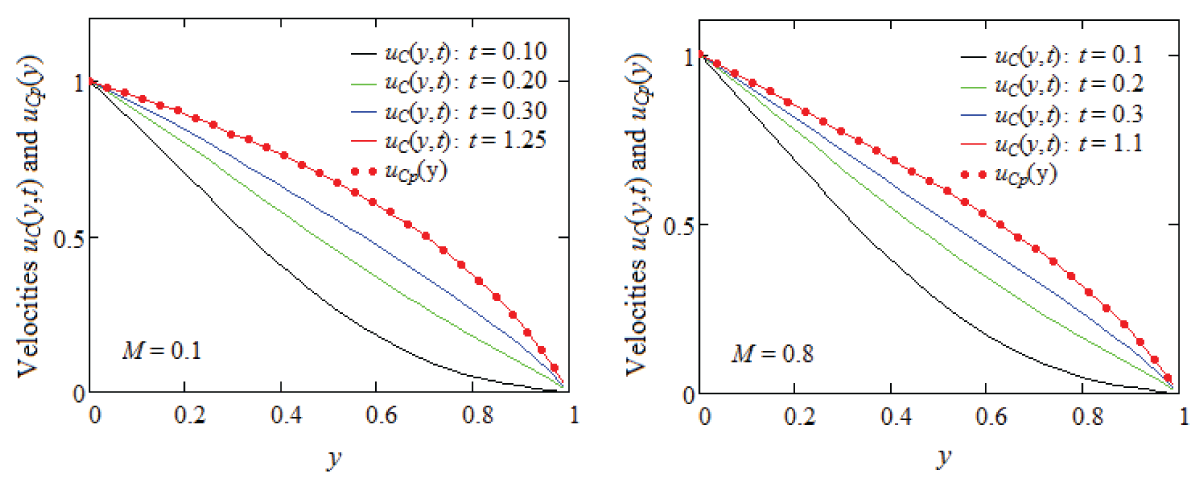
The analytical study examines the isothermal, unsteady flows of viscous incompressible fluids in a planar channel, when viscosity depends linearly on pressure, and a constant magnetic field is present. Exact expressions are derived for the dimensionless initial velocity field, the corresponding non-zero shear stress, and the problem is fully solved. To illustrate and highlight certain fluid behavior characteristics, modified Stokes’ problems are analyzed, and analytical expressions for the corresponding initial velocities are provided. For validation, the steady components are presented in two distinct forms, with their equivalence confirmed through graphical comparison. The effect of the magnetic field on the fluid behavior is explored and discussed visually. The results show that the fluid flows more slowly, and the steady-state is reached sooner when a magnetic field is applied.
2010 Mathematics Subject Classification: 76A05.